Kryptografia.0: OTP
Na całym poniższym wpisie została przeprowadzona dwukrotnie operacja XOR z tym samym kluczem szyfrującym.
Wstęp
Kryptologia – dziedzina wiedzy o przekazywaniu informacji w sposób zabezpieczony przed niepowołanym dostępem.
Kryptografia to po prostu sposoby na przekazanie informacji w taki sposób, aby tylko zamierzony przez nas odbiorca był w stanie ją odczytać. To tak jakbyś chciał, aby kolega z ławki obok przekazał liścik dziewczynie ławkę dalej która się Ci podoba, ale nie dowiedział się o tym, że udało się Ci umówić z nią na kawę, bo jemu też się koleżanka podoba.
Współczesną kryptografię można podzielić na dwa działy:
-
symetryczną
-
asymetryczną (klucza publicznego)
Kryptografia symetryczna
Symetria - gr. symmetría, od sým-metros współmierny
Współmierny, a więc mierzący tyle samo, równy temu samemu, będący tym samym. W tym przypadku chodzi o klucz wykorzystywany do zaszyfrowania i odszyfrowania wiadomości. W wielu, jeśli nie większości, czy wręcz wszystkich materiałach o szyfrowaniu jako pomoc w tłumaczeniu działania wykorzystywana jest analogia kłódek oraz kluczy, w tym również.
Korzystając z kryptografii symetrycznej, korzystamy z kłódkluczka, który pozwala jednocześnie na zamknięcie wiadomości w pudełku (zaszyfrowanie), jak i otwarcie pudełka (odszyfrowanie).
One-time pad
Szyfr klucza jednorazowego to bardzo prosty szyfr wykorzystujący dwie rzeczy: funkcję XOR oraz losowość. Co ciekawe jest on teoretycznie perfekcyjnie bezpieczny, a uściślając — szyfrogram (zaszyfrowana wiadomość) nie ujawnia żadnej* informacji o oryginalnej wiadomości. * Poza długością wiadomości.
⊕XOR
Funkcja logiczna eXclusive OR, czyli w języku polskim alternatywa wykluczająca to funkcja przyjmująca dwa bity na wejściu i mająca jedno bitowe wyjście, a tak wygląda tablica prawdy dla niej:
| Wejście | Wyjście | |
|---|---|---|
| A | B | |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
A więc prawdziwe są zapisy 1⊕1=0, 0⊕0=0, 1⊕0=1, 0⊕1=1
OTP
Jak sama nazwa wskazuje, korzystamy z jednorazowego klucza i to właśnie jego jednorazowość jest najważniejsza, zaraz zauważysz dlaczego. Załóżmy następującą sytuację:
Chcemy zaszyfrować wiadomość mab122 kluczem sekret, a więc w kodowaniu ASCII:
klucz = 01110011 01100101 01101011 01110010 01100101 01110100
wiado = 01101101 01100001 01100010 00110001 00110010 00110010
W tym momencie warto zauważyć największą bolączkę OTP. Klucz jest tej samej wielkości co wiadomość i w tym przykładzie może to nie mieć znaczenia, ale wyobraź sobie, że chcesz wysłać 16 GiB zdjęć koledze przez publiczny kanał komunikacji, gdybyś chciał to zrobić bezpiecznie musiałbyś przekazać mu w bezpieczny sposób również klucz, który również ma 16 GiB, a skoro i tak musisz bezpiecznie przesłać tyle danych to możesz równie dobrze po prostu przesłać w ten sam sposób zdjęcia.
Wracając, zastosujmy OTP wykonując operację XOR
klucz = 01110011 01100101 01101011 01110010 01100101 01110100
⊕
wiado = 01101101 01100001 01100010 00110001 00110010 00110010
=
szyfr = 00011110 00000100 00001001 01000011 01010111 01000110
Jeśli zdajesz sobie sprawę, że dalej mówimy o kryptografii symetrycznej to wiesz, że w celu odszyfrowania szyfrogramu potrzebujesz tego samego klucza. Jak to zrobić? Wykonać XOR szyfrogramu z kluczem!
szyfr = 00011110 00000100 00001001 01000011 01010111 01000110
⊕
klucz = 01110011 01100101 01101011 01110010 01100101 01110100
=
wiado = 01101101 01100001 01100010 00110001 00110010 00110010
A teraz finał, dlaczego jednorazowość i losowość jest taka ważna? Wyobraź sobie, że przez przypadek zaszyfrowałeś kolejną wiadomość tym samym kluczem.
wiado2 = 00100000 00100000 00100000 00100000 00100000 00100000
⊕
klucz = 01110011 01100101 01101011 01110010 01100101 01110100
=
szyfr2 = 01010011 01000101 01001011 01010010 01000101 01010100
Problem pierwszy, losowość, okazuje się, ze twoja wiadomość to same spacje, a kolejnym przypadkiem okazuje się że odległość w kodowaniu ASCII pomiędzy małymi a dużymi literami to wartość spacji (00100000=2^5=32). Właśnie zmieniliśmy nasz klucz z sekret na SEKRET, całkiem sekretnie prawda?
Problem drugi, jednorazowe użycie: Atakujący ma teraz dostęp do dwóch zaszyfrowanych wiadomości:
szyfr1 = 00011110 00000111 00001010 00000110 00001010 00000110
szyfr2 = 01010011 01000101 01001011 01010010 01000101 01010100
Jeśli okazałoby się, że atakujący poznał treść poprzedniej wiadomości, to ma już klucz podany na srebrnym złotym talerzu.
wiado = 01101101 01100001 01100010 00110001 00110010 00110010
⊕
szyfr2 = 01010011 01000101 01001011 01010010 01000101 01010100
=
klucz = 01110011 01100101 01101011 01110010 01100101 01110100
Operacja XOR działa tak samo w obie strony.
wiado1 ⊕ klucz ⊕ wiado1 = klucz
klucz ⊕ wiado1 ⊕ klucz = wiado1
Więc nawet jeśli treść kolejnej wiadomości nie została poznana przez atakującego, ma on wciąż do dyspozycji dwa szyfrogramy.
wiado1 ⊕ klucz = szyfr1
wiado2 ⊕ klucz = szyfr2
szyfr1 ⊕ szyfr2 = (wiado1 ⊕ klucz) ⊕ (wiado2 ⊕ klucz)
(wiado1 ⊕ klucz) ⊕ (wiado2 ⊕ klucz) = wiado1 ⊕ wiado2
szyfr1 = 00011110 00000111 00001010 00000110 00001010 00000110
⊕
szyfr2 = 01010011 01000101 01001011 01010010 01000101 01010100
=
wiad12 = 01001101 01000010 01000001 01010100 01001111 01010010
Teraz wiad12 to kombinacja wiad1 z wiad2, ze względu na to, że wiad2 składa się z samych spacji, otrzymujemy wiad1 = mbator przesuniętą o 32 w kodowaniu ASCII… czyli wiad2 = MBATOR. Oczywiście pokazany tutaj przypadek jest skrajny, ale mając do dyspozycji na przykład schemat zapisu, większą liczbę, czy treść którejś z poprzednich wiadomości jesteśmy w stanie wyczytać informację ze zmieszanych ze sobą treści.
Graficzny przykład
Świetną wizualizację tego zjawiska możemy znaleźć na blogu cryptosmith.com. Do zaszyfrowania mamy plik graficzny: 
Wygenerowaliśmy więc OTP tego samego rozmiaru:
XORujemy całość i otrzymujemy zaszyfrowaną wiadomość:
Co się stanie gdy użyjemy ponownie tego samego klucza do zaszyfrowania innej wiadomości?
Jak narazie obydwie wiadomości wydają się nie możliwe do odczytania. Jeśli jednak wykonamy XOR obydwu wiadomości ze sobą:
Otrzymamy:
Źródło: cryptosmith.com - Stream cipher key reuse
Szyfry strumieniowe
Skoro wiesz już, że istnieje coś takiego jak OTP i XOR, możemy kontynuować. Współczesne szyfry strumieniowe to nic innego jak OTP z generowanym według potrzeb kluczem na podstawie wcześniej ustalonego sekretu.
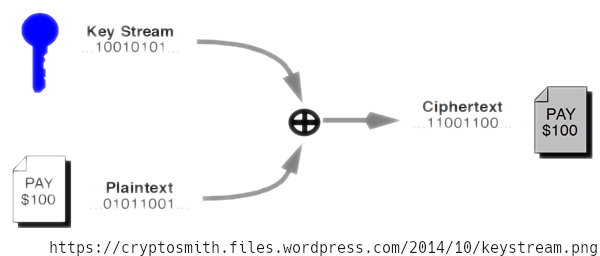W przeciwieństwie do szyfrów blokowych, szyfrowanie odbywa się bit po bit’cie to znaczy dla każdego bitu danych generowany jest bit klucza i wykonywana jest operacja XOR. W ten sposób wychodzący strumień wygląda na losowy i zdradza informację dopiero po odszyfrowaniu takim samym kluczem.
Ciąg dalszy w Kryptografia.1: Tryby szyfrowania blokowego