mbator.pl / Technologie informacyjne - kolokwium
Autor: Maciek Bator

Technologie informacyjne - kolokwium

Podstawy technologii informacyjnych w rozdrobnionej pigułce do wciągnięcia nosem.

Konwersja dec2bin, bin2dec

Wszyscy wiedzą, że komputery operują wyłącznie na zerach i jedynkach* I także wszyscy wiedzą, ze komputery to tak naprawdę skomplikowane kalkulatory Więc wypadałoby wiedzieć jak zamienić liczby z formy zrozumiałej dla nas na taką zrozumiałą przez komputer i na odwrót, aby móc odczytać wynik. A więc z zapisu dziesiętnego na binarny czyli zapisany za pomocą dwóch różnych stanów nie ważne jak opisanych, kreską i kropką, jedynką i zerem, niskim napięciem i wysokim napięciem, prawdą i fałszem.

Praktyka

Mając liczbę zapisaną w systemie dziesiętnym zapisujemy ją za pomocą dziesięciu rozróżnialnych symboli/stanów/jogurtów/frytek/kolorów/kształtów/czegokolwiek (polecam jednak tzw. arabskie).

0 1 2 3 4 5 6 7 8 9

Zamieniając liczbę na dwójkowy warto zapamiętać poniższe wartości:

2^7=128 2^6=64 2^5=32 2^4=16 2^3=8 2^2=4 2^1=2 2^0=1

Pozwolą nam one na zapisanie 8 bitowej liczby, każde wyliczenie powyżej odpowiada kolejnym bitom. Osobiście często zapisuję je sobie w takiej właśnie formie na kartce gdy zamieniam systemy liczbowe. Następnie aby zamienić liczbę np. 45, zauważamy, że jest ona nie parzysta co oznacza, że ostatni bit na pewno będzie jedynką

2^7=128 2^6=64 2^5=32 2^4=16 2^3=8 2^2=4 2^1=2 2^0=1
   ?       ?      ?      ?      ?     ?     ?     1

Następnie patrząc od lewej szukamy największego wyniku który jest mniejszy bądź równy naszej liczbie dziesiętnej.

2^7=128 2^6=64 2^5=32 2^4=16 2^3=8 2^2=4 2^1=2 2^0=1
   ?       ?      1      ?      ?     ?     ?     1

Podliczając nasza liczba binarna jest równa teraz 33, to wciąż za mało, potrzebujemy 45. Szukamy kolejnej liczby która będzie równa bądź mniejsza (45-33)=12.

2^7=128 2^6=64 2^5=32 2^4=16 2^3=8 2^2=4 2^1=2 2^0=1
   ?       ?      1      ?      1     ?     ?     1

32+8+1=41, wciąż brakuje nam 4

2^7=128 2^6=64 2^5=32 2^4=16 2^3=8 2^2=4 2^1=2 2^0=1
   ?       ?      1      ?      1     1     ?     1

32+8+4+1 = 45

Zamiana dowolnej liczby binarnej na dziesiętną jest trywialnym zadaniem, aby zamienić n-bitówą liczbę w systemie dwójkowym na dziesiętny rozpisujemy sobie 2^n 2^(n-1) ... 2^0 i sumujemy wyniki tam gdzie bity równe są 1

Bramki logiczne

Bramkami logicznymi nazywamy urządzenia implementujące funkcje/operacje boolowskie.

Algebra Boole’a

Najważniejsze co trzeba wiedzieć z algebry Boole’a to trzy podstawowe operacje, które przyjmują dwa argumenty i dają jeden wynik.

Bramki

Bramki to implementacje podanych wyżej operacji, z tych trzech prostych bramek możemy budować kolejne, a podstawowe z nich oznacza się następującymi symbolami: 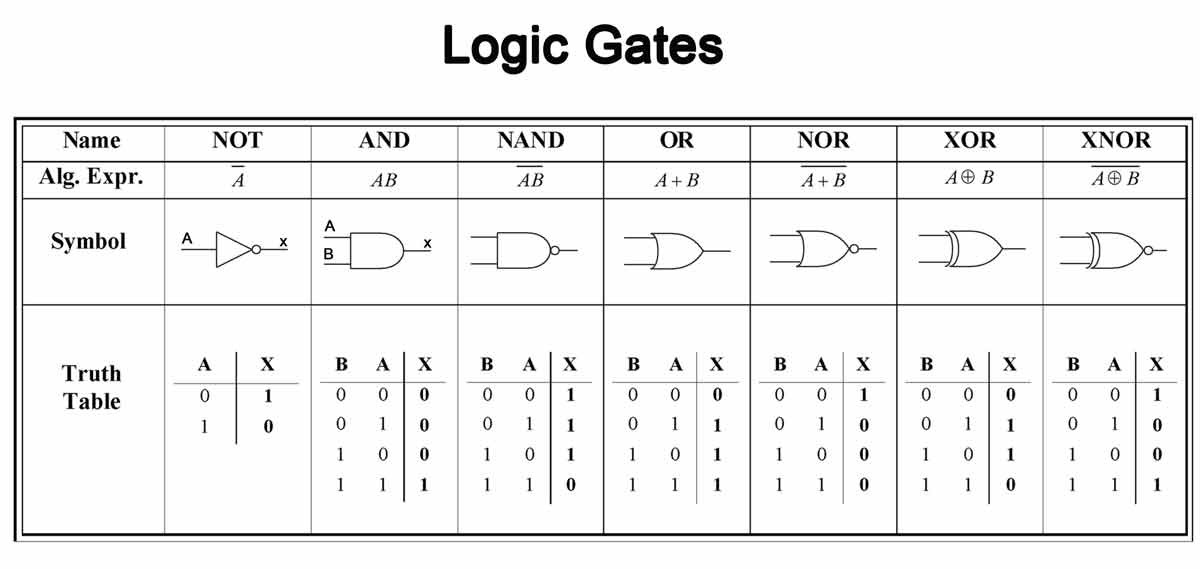Bramki logiczne z tabelkami prawdy Truth table w grafice powyżej (tabelka prawdy) pokazuje bezpośrednio suchymi faktami sposób działania bramki, kolumny oznaczone A i B oznaczają wejścia, czyli to co bramka/funkcja przyjmuje, a X to co „wypluwa” z drugiej strony.

Architektura komputera

W architekturze komputera wszystko rozbiega się o abstrakcję w poprzednim akapicie poznaliśmy bramki logiczne, które możemy układać i łączyć budując z nich proste komparatory, multipleksery, sumatory. Co najważniejsze, gdy zbudujemy już ten o jeden stopień bardziej skomplikowany układ, to zamykamy go w pudełku i przestajemy się nim przejmować. Potem z pudełek których faktyczna zawartość nas w ogóle ale to w ogóle nie obchodzi, budujemy bardziej skomplikowane układy. Interesuje nas tylko to że z jednej strony wrzucamy sygnały a z drugiej dostajemy przetworzone wyniki.

Architekture von Neumanna

Jedna z pierwszych architektur. Wyróżnia się współdzieloną pamięcią dla instrukcji i danych. Oznacza to, że procesor może ładować do pamięci jednocześnie albo dane albo instrukcje. architektura von Neumanna

Jeśli korzystałeś kiedyś z serwisu stackoverflow.com to ta nazwa oznacza, overflow (nadpisanie) części pamięci w której znajdują się instrukcje przez część danych (w ten sposób można doprowadzić do wykonania nie porządanych instrukcji). Jest to możliwe, ze względu na sposób w jaki system zarządza pamięcią. 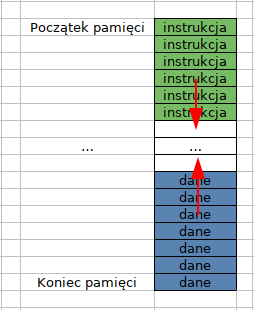Stack overflow Dane są zapisywane od dołu w górę (od najdalszego adresu po koleji w górę), a instrukcje od góry w dół (od adresu 0 po koleji w dół)

Architektura Harvardzka

Ta architektura wyróżnia się osobną pamięcią przeznaczoną dla instrukcji i dla danych. Oznacza to, że CPU może jednocześnie otrzymywać instrukcje i otrzymywać dostęp do danych. Nie jest także podatny na błędy typu stackoverflow. architektura Harvardzka

CISC

Complex Instruction Set Computing. Ten podział architektur odnosi się do Instruction Set-u komputera, jest to zbiór poleceń jakie procesor może wykonać jak nazwa wskazuje w tym przypadku jest on dość skomplikowany - co to oznacza? Polecenia, które wydajemu procesorowi są wyspecjalizowane i złożone, komputer zdejmuje jakby część programowania z ramion programisty na rzecz zaimplementowanych już bezpośrednio w krzemie gotowych poleceń. Istota tej architektury to, że my jako programista wydajemy jedno polecenie, które tak naprawdę może wymagać wykonania wielu podpoleceń dla przykładu:

Mówimy:
 Zsumuj liczbę A z liczbą B

A komputer tak naprawdę musi wykonać:
 Pobierz liczbę A z pamięci
 Pobierz liczbę B z pamięci
 Zsumuj liczbę A i B
 Zapisz wynik w pamięci

.

RISC

Reduced Instruction Set Computing. Wnioskując po tym co wiemy o architekturze CISC. Architektura Reduced Oddaje w ręce programisty tylko najbardziej podstawowe instrukcje, więc sami musimy pomyśleć o czytaniu i zapisywaniu do pamięci o tym gdzie co trzymamy i jak wykonywać bardziej skomplikowane operacje. Procesory na tej architekturze są jeszcze bardziej bezmyślnymi maszynami wykonującymi tylko nasze bezpośrednie i jasne polecenia.

Algorytmy, schematy blokowe, pseudokod

Algorytm – skończony ciąg jasno zdefiniowanych czynności koniecznych do wykonania pewnego rodzaju zadań, sposób postępowania prowadzący do rozwiązania problemu

~ encyklopedia PWN

Jak można przedstawić algorytm? Za pomocą pseudokodu. Przykład:

jeżeli numer karty kredytowej jest ważny to
    wykonanie transakcji w oparciu o numer karty i zamówienie 
w przeciwnym razie
    wyświetlenie wiadomości o niepowodzeniu
koniec warunku

Przykładowej implementacji:

<?php
if (karta_wazna($nr_karty)) {
    wykonaj_transakcje($nr_karty, $zamowienie);
} else {
    informacja_o_bledzie();
}
?>

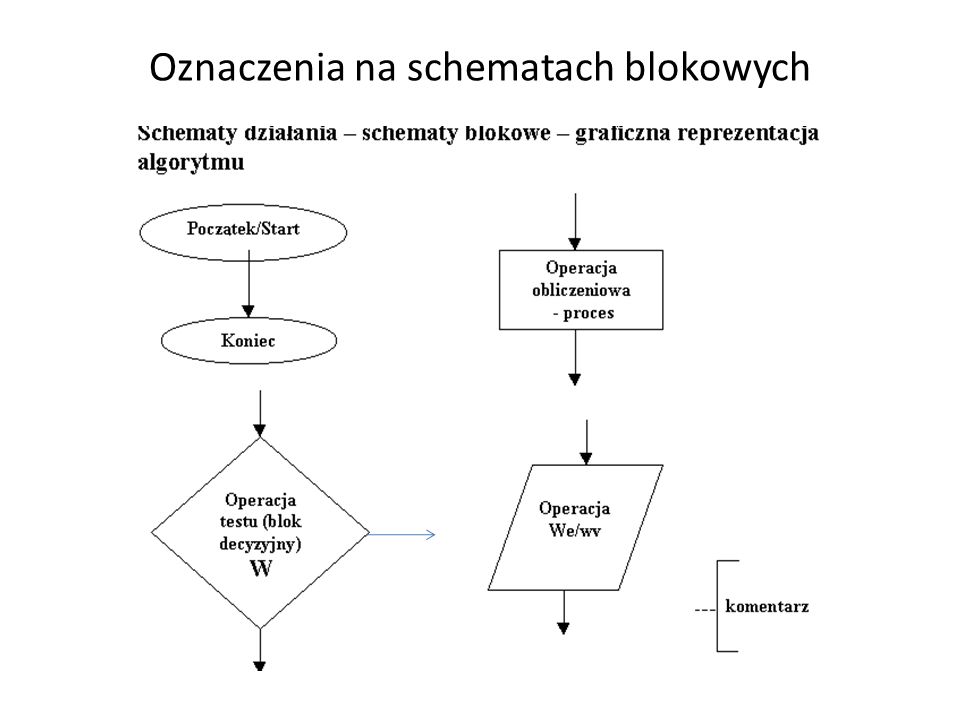
Za pomocą schematów blokowych: Schematy blokowe

Bezpieczeństwo danych, hasła

Bezpieczeństwo danych zależy od sposobu ich przechowywania, nośnika na którym je przechowujemy. Dane możemy podzielić na te trzymane offline i online, te pierwsze z definicji są nie dostępne bezpośrednio z żadnego systemu informatycznego (np. pendrive w szufladzie), do tych drugich możemy uzyskać dostęp przez system informatyczny (np. pendrive wpięty do komputera).

Kolejnym zabezpieczeniem danych są uprawnienia nadane konkretnym plikom, katalogom i egzekwowane przez system operacyjny. Są one bezużyteczne w momencie gdy uruchomimy inny system czy przełożymy dysk/pendrive do innego urządzenia.

W celu uchronienia się przed takim sposobie odczytania danych przez osoby nie pożądane możemy dane zaszyfrować i to jest temat rzeka. Zasadniczo duże ilości danych zabezpieczamy szyframi symetrycznymi (a więc takimi które do zarówno do szyfrowania jak i deszyfracji wymagają tego samego klucza/hasła).

hasła

Bezpieczne hasło musi spełniać tak naprawdę tylko i wyłącznie dwa warunki:

  1. Muszą pozostać sekretem.
  2. Muszą być jak najbardziej nieprzewidywalne Hasła mogą być atakowane na różne sposoby:
    • słownikowy - atakujący ma bardzo długą listę różnych możliwych haseł i sprawdza je wszystkie po kolei
    • brute-force - siłowy - atakujący generuje po kolei kolejne wariacje i sprawdza je np. aaaaa, aaaab, aaaac, ..., haslm, hasln, haslo
    • atak hybrydowy - połączenie powyższych i wariacje na ich temat na przykład modyfikowanie haseł z listy i sprawdzanie ich

Od wielu lat było wpajane i wymagane od nas, użytkowników wymyślanie zmyślnych haseł, które muszą zawierać małe litery, duże litery, znaki specjalne i mają odpowiednią długość. Takie hasła są bardzo trudne do zapamiętania przez ludzi (maszyny nie mają z tym problemu) co doprowadziło do uschematyzowania wymyślanych przez ludzi fraz (np. duża litera jest zawsze na początku).

Okazuje się że dużo lepszym rozwiązaniem jest chociażby wylosowanie sobie np. 8 wyrazów ze słownika, są one o wiele prostsze do zapamiętania niż ciąg losowych liter i znaków specjalnych. Należy tu jednak zaznaczyć, że wyrazy muszą zostać wylosowane, nie może to być zdanie z jakieś książki czy wiersza (wtedy byłoby łatwe do odgadnięcia).

Długość hasła ma oczywiście znaczenie, im krótsze hasło tym mniej prób w ataku _brute-force musi wykonać atakujący, co przekłada się na krótszy czas łamania tego hasła. Od 12 znaków (bądź w przykładzie powyżej 12 wyrazów) czas łamania (zakładając, że znaki są losowe i nie działa metoda słownikowa) może wynieść nawet do 2 stuleci.

TL;DR

podsumowanie w sproszkowanej pigułce

dec2bin, bin2dec

2^7=128 2^6=64 2^5=32 2^4=16 2^3=8 2^2=4 2^1=2 2^0=1
   0       0      1      0      1     1     0     1

32+8+4+1 = 45

bramki logiczne

A i B wejścia, X wyjście

Obrazek

architektura komputera

algorytmy

skończony ciąg jasno zdefiniowanych czynności koniecznych do wykonania pewnego rodzaju zadań, sposób postępowania prowadzący do rozwiązania problemu

Obrazek

bezpieczeństwo danych, hasła

Dane można:

(wtedy zmiana systemu, bądź przeniesienie danych na inny system (przepięcie pendrive) pozwala na ich odczyt)

Hasła muszą: